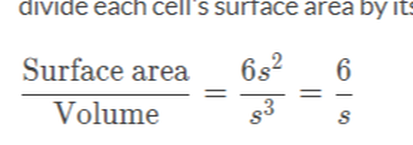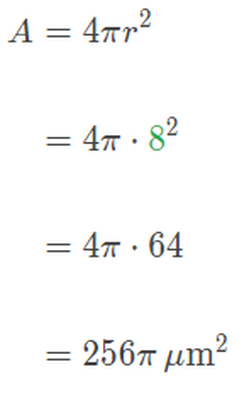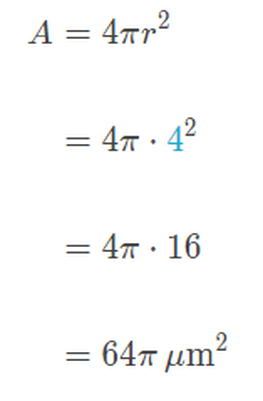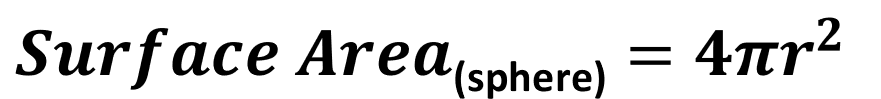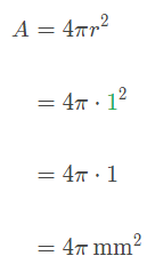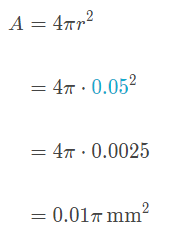Lab 1 - Surface Area to Volume Ratios
Major Concepts
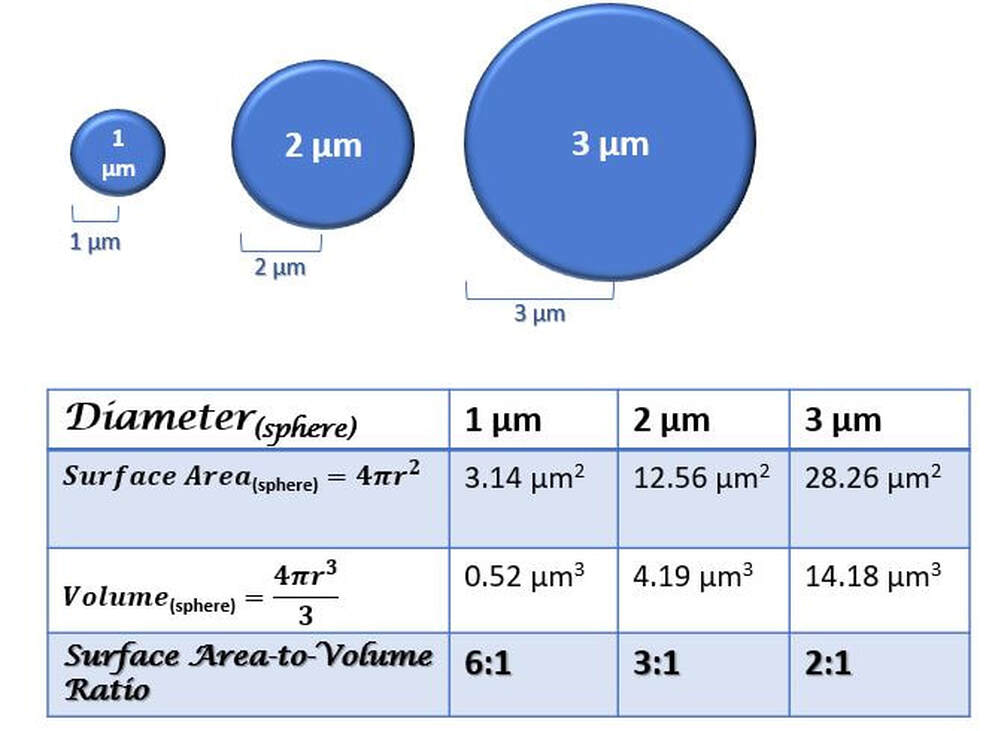
- As the surface area and the surface-to-volume ratio of a cell increases, so does its ability to exchange materials. The rate increased almost linearly with increasing surface-to-volume ratio.
- As cells perform their normal functions, they need to exchange materials with the world outside of the cellular membrane. Cells with larger surface-to-volume ratios are able to exchange materials more efficiently.
- The smaller a cell, the larger its surface-to-volume ratio. As a cell grows larger, the volume increases faster than the surface area. Small cells are more efficient at exchanging materials than large cells because they have more surface area to work with in relation to their size.
- In the small intestine, the surface is covered by epithelial cells that have increased their surface areas by forming tiny folds of their cellular membrane called microvilli. The microvilli dramatically increase the surface area of these cells and their ability to absorb nutrients. In general, cells adapt to the task of absorption and excretion by increasing the size of their cellular membrane while keeping their volume low.
- As cells grow larger, their volume increases faster than their surface area. This leads to a decrease in the efficiency of the cell at exchanging materials across the cell membrane.
- To be able to efficiently exchange materials, cells must divide by mitosis and cytokinesis when they become too large.
https://www.khanacademy.org/science/ap-biology/cell-structure-and-function/cell-size/v/scale-of-cells
|
|
|
|
|
|
The physical characteristics of a cell influence how it functions.
Practice Problem #1
For example, the surface area and volume of a cell affect how efficiently waste is removed from the cell via diffusion.
The table below shows data for four different cuboidal cells.
The table below shows data for four different cuboidal cells.
Using the information from the table, what is the surface-area-to-volume ratio for the cuboidal cell that removes waste via diffusion most efficiently?
|
HERE'S A LITTLE HINT!!
A cell removes waste via diffusion more efficiently when it has a higher surface-area-to-volume ratio. To calculate the surface-area-to-volume ratio for each of the cuboidal cells, we need to divide each cell's surface area by its volume: Cell A has the highest surface-area-to-volume ratio, so it must remove waste via diffusion most efficiently. So, the answer is the surface-area-to-volume ratio of cell A, which is 6um -1 |
|
Practice Problem #2
Humans are made up of many types of cells, and these cells have a broad range of sizes.
For example, an immune system cell called a neutrophil has a radius of approximately 4μm, while a type of connective tissue cell called a fibroblast has a radius of about 8μm.
Using the Formula for the Surface Area of a Sphere:
Assuming both cell types are perfectly spherical, how many times larger is the surface area of a fibroblast compared to the surface area of a neutrophil?
For example, an immune system cell called a neutrophil has a radius of approximately 4μm, while a type of connective tissue cell called a fibroblast has a radius of about 8μm.
Using the Formula for the Surface Area of a Sphere:
Assuming both cell types are perfectly spherical, how many times larger is the surface area of a fibroblast compared to the surface area of a neutrophil?
First, let’s calculate the surface area of a fibroblast.
A fibroblast has a radius of 8μm. |
Next, let’s calculate the surface area of a neutrophil.
A neutrophil has a radius of 4μm. |
Finally, let’s calculate how many times larger the surface area of a fibroblast is compared to the surface area of a neutrophil by dividing the two values:
So, a fibroblast has 4 times more surface area than a neutrophil.
Practice Problem #3
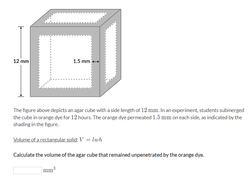
Because the orange dye permeated the agar cube equally on all sides, the inner, unpenetrated portion of the agar cube is also cube-shaped.
To find the volume of this inner cube, we first need to calculate its side length.
To do so, let's subtract the permeation distance of the orange dye 1.5mm on each side from the total side length of the agar cube 12mm.
To find the volume of this inner cube, we first need to calculate its side length.
To do so, let's subtract the permeation distance of the orange dye 1.5mm on each side from the total side length of the agar cube 12mm.
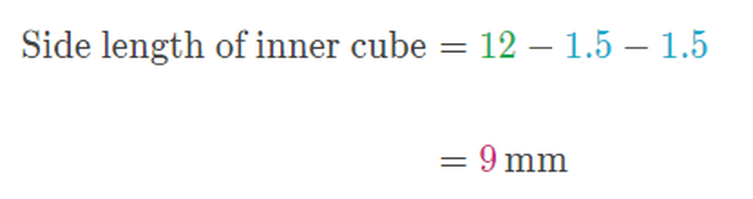
Next, using the side length we calculated, we can find the volume of the inner cube.
Because all sides of a cube have the same length, we know that the length, width, and height of the inner cube are all 9mm.
Using the formula for volume of a rectangular solid, which is...
V = lwh =9 x 9 x 9 = 729mm3
So, the volume of the agar cube that remained unpenetrated by the orange dye is 729mm.
Because all sides of a cube have the same length, we know that the length, width, and height of the inner cube are all 9mm.
Using the formula for volume of a rectangular solid, which is...
V = lwh =9 x 9 x 9 = 729mm3
So, the volume of the agar cube that remained unpenetrated by the orange dye is 729mm.
Practice Problem #4
Cell Y has a surface area 240μm squared, and a volume of 8μm cubed.
Cell Z has a surface area of 72μm squared and a volume of 12μm cubed.
Using the information above, determine the surface-area-to-volume ratio of each cell. What is the SA:V ratio of the cell that will exchange materials with its environment at the fastest rate of diffusion?
Cell Z has a surface area of 72μm squared and a volume of 12μm cubed.
Using the information above, determine the surface-area-to-volume ratio of each cell. What is the SA:V ratio of the cell that will exchange materials with its environment at the fastest rate of diffusion?
Practice Problem #5
An oocyte is an immature reproductive cell found in many sexually reproducing organisms. A crawfish oocyte has a radius of approximately 1mm, while a human oocyte is much smaller and has a radius of about 0.05mm.
Assuming both cell types are perfectly spherical, how many times larger is the surface area of a crawfish oocyte compared to the surface area of a human oocyte?
First, let’s calculate the surface area of a crawfish oocyte. A crawfish oocyte has a radius 1mm. |
Next, let’s calculate the surface area of a human oocyte. A human oocyte has a radius of 0.05mm.
|
Finally, let’s calculate how many times larger the surface area of a crawfish oocyte is compared to the surface area of a human oocyte by dividing the two values:
